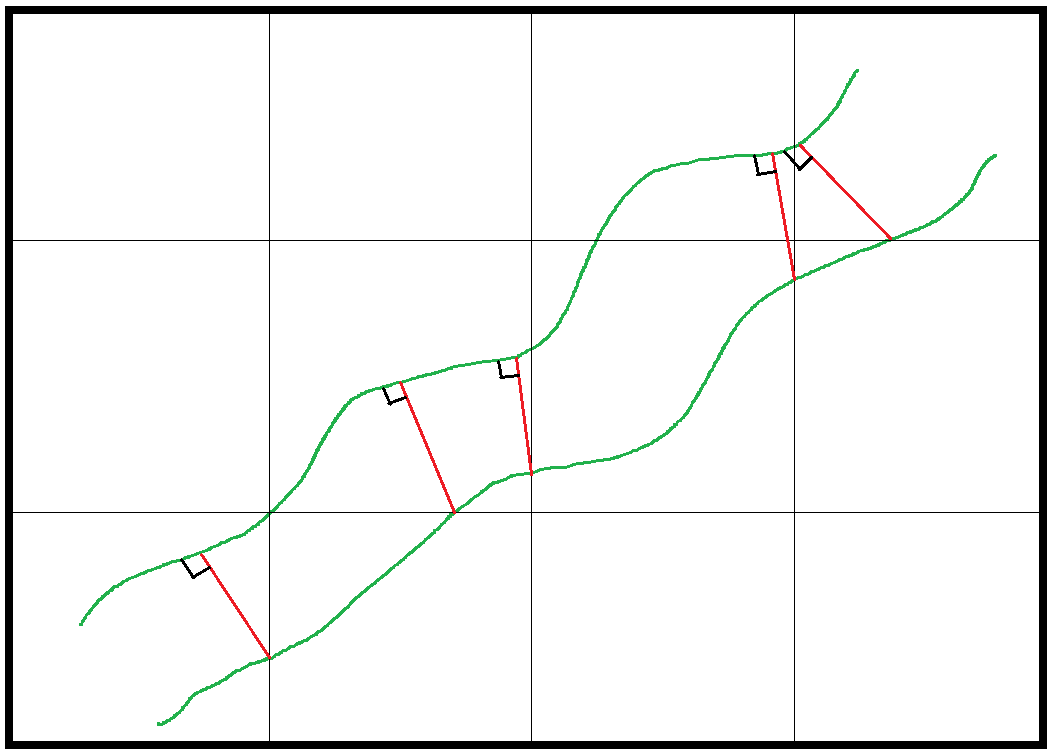

To estimate thickness, for instance the thickness of the interhemal membrane in the placenta that separates the maternal from the fetal blood, the Orthogonal Intercepts probe (Jensen, et al., 1978) is appropriate. As usual for unbiased stereology, systematic random sampling is used. This probe consists of making measurements of the thickness, and the places where those measurements are started are indicated by a grid. The grid is put over the tissue, and the places to start the measurements are where a grid line intercepts one side of the membrane or object whose thickness is being estimated. To avoid projection problems, use thin physical or optical sections (Jensen, et al., 1978, Fig. 3). To make a measurement, start a line-segment from one side of the membrane as indicated by the intersection of the grid. Extend it to the other side such that it intercepts orthogonally; this will be the shortest distance across the membrane in that particular section. This line-segment is the orthogonal intercept (see red line-segments in figure below). No orthogonal intercept can be traced on an island or from a wave, and if there is more than one possible direction an orthogonal intercept can be made, trace the shortest one (Jensen, et al., 1978, Fig. 4.).
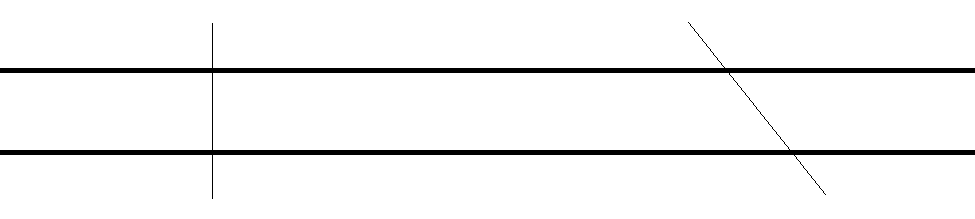
Despite the fact that we have made our tissue orientation isotropic, the thickness will be overestimated, since not all sections will be perpendicular to the membrane surface. These non-perpendicular cases of sectioning will cause the thickness to appear longer than it is, in other words, we can only appreciate the real thickness when the section is perpendicular to the surface. In the figure below, we can see that the cross-section that is not perpendicular to the surface (thin line on right going through membrane indicated by parallel thick lines) will overestimate the membrane thickness, while the cross-section that is perpendicular (thin line on left) will not.
To correct for this multiply the observed/measured thicknesses by π/4 for the arithmetic mean thicknesses (Jensen, et al., 1978, equation 9) or the harmonic mean thicknesses by 8/(3*π) for the harmonic mean values (Jensen, et al., 1978, equation 10).
T = π/4 (L0) for mean thickness
T = 8/(3*π) (Lharmonic) for harmonic mean thickness
T = estimated thickness
L0 = observed/measured thickness mean
The harmonic mean, Lharmonic, is the reciprocal of the mean of the reciprocals of the observed/measured thicknesses, L0.
The harmonic mean emphasizes the minimum thicknesses; the effect of adding large thicknesses is diluted compared to the regular mean. Notice that the multiplication factor is larger for the harmonic thickness (8/(3*π) = 85%, see Jensen, etal., pg. 22, last sentence before section 2) than for the arithmetic mean (π/4 = 79%); it is the shorter harmonic mean length that will make the harmonic mean thickness smaller. The harmonic mean thickness is especially relevant for membranes that have to do with diffusion, and it is inversely proportional to the diffusing capacity. For instance see (Coan, et al., 2004, ‘Interhemal Membrane Thickness’ and ‘Morphometric Diffusing Capacity of the Interhemal Membrane’). For an example in lung, please see (Ferrando, et al., 2003), where the thickness of the basement membrane in bronchial biopsy tissue is estimated.
For information on how to estimate width or thickness indirectly, please see ‘estimating width of slabs‘.
____________________________________________________________________

Sponsored by MBF Bioscience
developers of Stereo Investigator, the world’s most cited stereology system