or ……. Why is there a Two in the Length and Surface Estimation Formulas?
Unbiased estimates of length and surface can be obtained using design-based stereology. In Biology, microscopic images that are viewed in a systematic and random way are examined using geometrical shapes called probes. For length and surface the interaction of the probe and feature must be isotropic; no particular orientation can be favored. To estimate, per volume, the length of strings, such as blood vessels or nerves, we probe with surfaces. To estimate surface areas, such as biological membranes, per volume, line segment probes are used. The following relationships hold (Stereology Symbols):
Lv = 2Q/A
Lv is length per volume
Q is number of intersections of the surface probe with the string
A is area of the surface used to probe with
and
Sv = 2I/L
Sv is surface per volume
I is number of intersections of the line-probe with the surface
L is length of the line-segment probes
The number of intersections encountered is proportional to how much length or area there is. This makes sense on an intuitive level, the more times the probe hits the strings or surfaces, the more there is. Even ants know this (Mallon and Franks, 2000). So it makes sense that intersection, I or Q, is in the numerator of these formulas. It also can be appreciated on a gut level that the size of the probes will affect the estimate. If the same number of intersections is obtained with a larger probe, there is less length or surface present. That is why the area of the probe for length (A) and the length of the probe for surface (L) is in the denominator of these formulas. But where does the two come from? Why is it twice the number of intersections per probe size that gives an estimate of the length or the surface per volume?
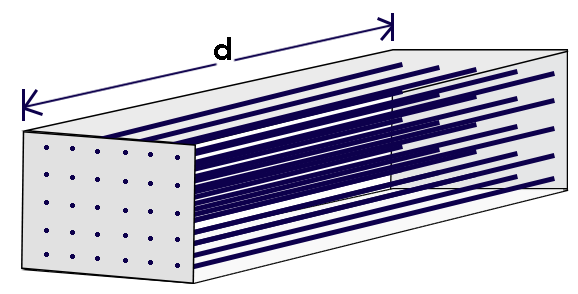
We can try to approach understanding these formulas in a conceptual way (Tang and Nyengaard, 2004, chapter 12, section 1.1). Let’s concentrate on length. Think about estimating the length of strings. Picture the strings all parallel to each other, in a rectangular volume, lined up with the long axis and perfectly straight. Picture a box of store-bought spaghetti:
If you take a cross-section you will see intersections and the length of all the strings equals the long dimension of the rectangular volume (call it d) times the number of intersections. In other words, because of this special case where the strings are parallel and straight, and our probe, the plane created by the cross section, is perpendicular, the number of intersections is the number of strings and d is the length of each string:
length of all strings = d(number of intersections)
d is the long dimension of the rectangular box
Divide by the volume of the rectangular box to get length per volume. The volume of the box is the cross-sectional area times the long dimension:
length of strings per volume = [d(number of intersections)] / [d(cross sectional area of box)]
= number of intersections / area
But this is the result if the probe, the surface created by taking a cross section, is perpendicular to the strings. What if the cross section had been parallel to the strings? No intersections would result and we would think there is nothing there. “The constant ‘2’ in the correct length estimation formula is a consequence of the 50% chance of linear structures in three-dimensional space being intersected by a uniform randomly orientated plane” (Tang and Nyengaard, 2004, p. 251). Therefore, and this can be grasped on an intuitive level, this formula underestimates length. That is why the ‘two’ is added, to ‘make up for’ this underestimation; but in my opinion the choice of two is not so obvious.
So let’s try to understand, on a mathematical level, why the ‘two’ is in the formulas. Where did these formulas come from? They are certainly well accepted; Baddeley, Gundersen and Cruz-Orive (1986, p. 261) refer to these relationships as “familiar facts”. The reference I have often seen given is from Saltykov from 1946; which is published in Russian. We have to go back much farther in time though to get to an origin of these formulas, to the 1777 paper from George Louis Leclerc, Comte de Buffon, published in French. Cruz-Orive (1997, section 3.1, From Buffon to the Spatial Grid of Planes, p. 96) writes that the problem that Buffon proposed and solved “encapsulates the essence of geometrical probability, and lies therefore at the root of stereology”. All discussion here is ‘after Saltykov’ and ‘after Buffon’ mostly from Cruz-Orive (1997) and Smith and Guttman (1953) but there is also a derivation in Gokhale, 1989 (Section 2, Theory, p. 134).
What Buffon did was to empirically figure how the probability of the occurrence of an intersection is affected by the size of the probe relative to the amount of strings or surface that is being studied. He used a two-dimensional model system; a floor with floorboards. The cracks formed by the joining of the boards were at a known distance from each other, ‘h’. He used a line-segment of a known length, referred to as a ‘needle’, whose length, ‘b’, was less than the spacing among floorboard cracks. He threw the needle down over and over again in a random way to assure an isotropic interaction and kept track of the number of intersections with the floor board cracks verses the number of throws.
How does the length of the needle and the distance between the lines on the floor relate to the probability of an intersection? This probability is the number of favorable outcomes, meaning intersections, divided by all possible outcomes, meaning the number of throws. The longer the needle, the more likely there will be an intersection, so b is in the numerator. The farther apart the parallel lines on the floor are; the less likely is the chance for an intersection, so h goes in the denominator. Buffon found that the probability of an intersection using an isotropic and random toss is equal to twice the length of the needle divided by π and the spacing of the lines on the floor, this is where the ‘two’ comes from for two-dimensional length esimation formulas:
probability of an intersection = number of intersections/number of throws = [2/π] [b/h]
b is the length of the needle
h is the distance between the lines on the floor
You can try this for yourself, and there are web-pages that will let you ‘toss the needle’ virtually. We did it here at MBF Bioscience using a 20 cm stick (b = 20 cm.) and a plane with parallel lines spaced at 30 cm (h = 30 cm.). Over the course of a couple of weeks, many of us threw the stick onto the plane in such a way that we could not control how it landed; usually by spinning it as we threw it. If we had managed to throw the 20 cm stick an infinite amount of times in a perfectly isotropic way, there would be a 42% chance of an intersection:
[2/π] [b/h] = [2/π] [20cm/30cm] = 0.42 = 42%After just 176 tosses we came close to what Buffon demonstrated, obtaining 81 intersections.
Probability of an intersection = number of intersections / number of throws
= 81/176
= 46 %
Cruz-Orive (1997, section 3.1, From Buffon to the Spatial Grid of Planes, p. 96) talks about the probability of an intersection as the number of favorable cases divided by the number of possible cases. The distance between the lines on the floor, h, can be thought of a measure of all possible positions of the thrown needle; if h = 0 there are no possible positions and if h = infinity, there are infinite possible positions. Twice the length of the needle, 2b, divided by π, or the average orthogonal projection of the needle on a perpendicular axis (Smith and Guttman, 1953, equation [1], p. 82 , note the needle length is called l instead of b by Smith and Guttman), is a measure of all favorable cases.
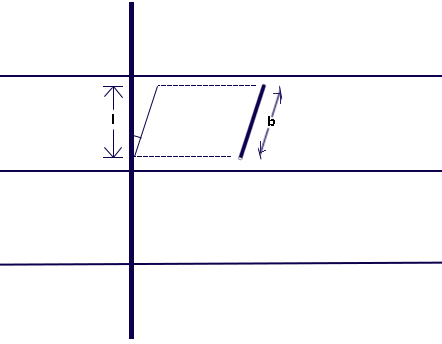The projection (l in the figure above) is equal to the length of the needle (b) times the cosine of the angle between the needle and the perpendicular axis. When the needle is parallel to the perpendicular axis it is perpendicular to the lines on the floor, giving the best chance for an intersection. When the needle is perpendicular to the axis and thus parallel to the floorboards, there is the least chance for a favorable position. The angle must be isotropic and the distance from the center of the needle to the lines on the floor must be uniform random. Isotropic-uniform-random is abbreviated as IUR (Miles and Davies, 1976).
Buffon was able to empirically show the relation between the length of the needle, the distance between the cracks on the floor and the probability for an intersection; but how do we go from that to the formulas for estimating length and surface? Smith and Guttman (1953, p. 82) explain that if “an irregular plane curve” is probed with an array of parallel lines, we can look at the curve as a series of “nearly straight” short segments (∆l). Each segment will be random in position and orientation as long as the whole curve is; therefore the probability for each may be summed. “The probability that any one of these intersects the array is
pi = 2*∆l/pi*d”
pi is the probability that a short segment of the curve will intersect the parallel lines
∆l are nearly straight short segments
d is the distance between the lines (switching to the nomenclature in Smith and Guttman)
and the product of this with the number of segments is the average number of intersections:
average N = pi * (l/∆l) (Smith and Guttman, 1953, equation 3)
N is the number of intersections
l is the length of the curve made up by ∆l
when we consider the whole curve, l/∆l is equal to one and:
average N = 2*l/π*d (Smith and Guttman, 1953, equation 3)
in practical terms it is useful to express the equation above in terms of a ratios of length to area. Consider an area, ‘A’, crossed by parallel probe lines, separated by the distance, ‘d’. “If d is small, or if a coarse grid is applied many times at random to a fixed area, the total length of grid line, L, is A/d” (Smith and Guttman, 1953, p. 82). Substitute A/L for d:
l/A = π/2 (average N)/L (Smith and Guttman, 1953, equation 4)
The length per area of a two-dimensional curve probed with line-segments of length L is π/2 times the average number of intersections encountered divided by the length of line-segment-probes.
Here are examples of formulas used to estimate length in two dimensions that can be recognized from the above formula. A “classical stereological equation” is (Cruz-Orive, 1997, section 3.1, From Buffon to the Spatial Grid of Planes, p. 96):
BA = π/2 (IL) (Cruz-Orive, 1997, equation 3.1)
BA is boundary per area
IL is intersections per length of line-probe
Or in a slightly different form, useful if you are probing for boundary length or 2-D length with a grid of lines:
B = π/2 (T) I (Howard and Redd, 2010, equation (2.5)
T = distance between lines in grid
I = number of intersections between grid lines and boundary
To be more efficient, an array of Merz half-circles can be used on a known fraction of the sample (Howard and Reed, 2010, equation 12.2):
Estimate of L = π/2 (a/l) (1/asf) (I) (see the Petrimetrics probe, Howard and Reed , 2010, Chapter 12)
L is length
a/l is the reciprocal of the length per area of the probe-lines
1/asf is the reciprocal of the area fraction
I is the number of intersection
We have looked at how Buffon’s idea relates to formulas for estimating length in two dimensions; let’s move on to three dimensions. Think of parallel planes in three-dimensions instead of lines on a floor (Cruz-Orive, 1997, section 3.1, From Buffon to the Spatial Grid of Planes, p. 96). What is the chance that a ‘needle’ of length, l, will intersects with parallel planes separated by a distance of ‘h’? Now we have to add an angle:
Theta is the angle between the perpendicular axis and the needle. Phi is the angle around the perpendicular axis. To ensure isotropy, theta must be randomly picked between 0 and 90 degrees, but then phi must be sin-weighted. In other words, an element of area on a sphere defined by phi and theta is not simply [d(theta)*d(phi)], instead it is [(sin theta)d(theta) * d(phi)]. The length of a projection on the perpendicular axis (lp) is a measure of favorable positions or hits of the needle on the planes.
lp = l * cos(theta) = the integral from 0 to 90 degrees of l * cos(theta) sin(theta)d(theta) = l/2
lp is the projection of the needle on the perpendicular axis
l is the length of the needle
theta is the angle between the needle and the perpendicular axis
Since ‘h’, the distance between the planes, is a measure of all possible positions:
probability of an intersection = favorable positions/all possible positions = (l/2)/h = l/2h (Cruz-Orive, 1997, section 3.1, From Buffon to the Spatial Grid of Planes, pp. 96-97).
h is the distance between planes
This is where the two comes from in the three dimensional length estimation equations: the mean projected length of the needle on an axis normal to the planes is l/2. Now we can use the same reasoning as for the two-dimensional situation. Instead of a ‘needle’ consider a curve. It can be broken down into almost straight segments, and they will be IUR as long as the curve is IUR. Therefore the probabilities of an intersection with the parallel planes are additive. If we consider the whole curve, the average number of intersections will be:
average N = l/2h
N is the number of intersections
l is the length of the curve
h is the distance between planes
and the average area of the parallel planes within a given volume, V, is V/h. Substitute V/A for h:
l/V = 2 * average N/A
l is length of curve
V is volume
N is number of intersections
A is area of planes
also see:
Lv = 2Q/A (Cruz-Orive, 1997, equation 3.3)
We finally arrive at the relationship: the length per volume is equal to the number of intersections counted per area of probe. This equation is considered to be due to Saltyokov (1946) and rediscovered by Smith and Guttman (1953) (Baddeley and Jensen, 2005, section 2.11, bottom of page 52).
Using systematic and random sampling and sections that are a couple of microns thin, you can count the number of intersections per area to come up with an estimate of length per volume (see ‘Image Plane as Probe‘, Evans et al., 2004, section 3.3, p. 255 and Howard and Reed, 2010, p. 126). The strings have to be isotropic for this to be unbiased. If you don’t want to make your tissue isotropic by spinning it randomly in three planes, use sections that are thick enough to fit in a virtual sphere (see ‘Spaceballs‘, Mouton et al. 2002); this way the probe is isotropic so the tissue does not have to be (see preferential sectioning)! Here is the equation for estimating length with virtual spheres:
L = 2 (Σ Qi ) * v/a * 1/ssf
Qiis number of intersections of the surface of the virtual sphere with the strings
v is the volume of a cube associated with the virtual sphere
a is the surface area of the virtual sphere
ssf is the section sub-fraction
Notice it can be rearranged so as to recognize its origins in this equation: Lv = 2Q/A.
To get to the three dimensional equation for surface per volume, Cruz-Orive (1997, section 4.1, From Saltykov to Sandau, p. 98) tells us to take the formula for length per volume and consider the “dual situation”; after some notation changes we end up with:
SV = 2IL (Cruz-Orive, 1997, equation 4.1)
Surface area per volume equals twice the number of intersections counted per length of probe.
For fun, lets look at the way Smith and Guttman (1953, p. 83, see fig. 6) arrive at the above equation by deriving the relationship for a plane figure that is probed with parallel planes instead of a ‘needle’ that is probed with parallel planes. The intersection of a plane with a plane is a line segment. The length of that line-segment will be dependent on the distance between the planes, in this case we call it z, and the angle between the parallel planes and the plain-figure, theta. The element of surface, dz, “that is projected on a plane which includes the intersection and which is normal to the stack of planes” is equal to the product of a small increment of surface and the sin of the angle between a normal to the surface being probed and a normal to the stack of probing surfaces. The only relevant angle is theta. The average length of the intercept is obtained by integrating the relevant parameters pertaining to Z and theta to get:
average length = π * S/ 4 * d (Smith and Guttman, 1953, equation 6)
average length refers to the intercept between the parallel planes and the plane figure being probed
S is the surface of the plane figure
d is the distance between parallel planes
but d = V/average A
V is volume
A is area
so:
average length per average area = π/4 * S/V (Smith and Guttman, 1953, equation 7, also see the discussion of events for estimating surface)
But it is not as efficient to trace a line as it is to mark an intersection, and from our two-dimensional discussion above we know that:
l/A = π/2 (average N)/L
Substitute the right side of this equation for the left side of the one above and rearrange and we get:
S/V = 2*average N/L (Smith and Guttman, 1953, equation 8)
If you use systematic and random sampling and probe on sections that are a couple of microns thin with an array of half-circles, you can count the number of intersections of the half-circles with the surface (see Merz probe, Weibel, 1979, section 8.8, Robert K. Schenk, Bone tissue). The surfaces will have to be isotropic in this case. If vertical sections that are a couple of microns thin are used, surface can be probed with a special type of line segment called a cycloid. The vertical section is random in two planes and the cycloid is placed randomly but with respect to the vertical direction (see cycloids for Sv, Baddeley, Gundersen, and Cruz-Orive, 2005). In this case the formula is:
Sv = 2 * (p/l) * ΣI/ΣP
Sv is surface area per volume
p/l is the number of points per unit length of cycloid
I is the number of intersections counted
P is the number of points counted
If sections that are thick enough to contain an Isotropic Fakir (Kubínová and Janácek, 1998) probe are used, the tissue does not have to be isotropic or vertical, it can be in a preferred orientation, you can section it any way you like. This is because the probe itself, a triplet of mutually orthogonal line segments, is isotropic. Here is the equation for estimating with the Isotropic Fakir probe:
S = 2 * (1/n)* Σ (v/l) * I
S is surface
you know why the ‘2’ is there
n is the number of line segments (3)
v/l is the inverse of the probe density which is length per unit volume
I is the number of intersections you count
Notice how this equation can be rearranged to identify its progenitor: SV = 2IL .
Baddeley, A.J., Gundersen, H.J.G., and L.M. Cruz-Orive (1986). Estimation of Surface Area from Vertical Sections. J. of Microscopy, 142, 259-276.
Baddeley, A. and E.B.V. Jensen (2005). Stereology for Statisticians. Chapman and Hall/CRC, Boca Raton, Florida.
Buffon, G. “Essai d’arithmétique morale.” Histoire naturelle, générale er particulière, Supplément 4, 1777.
Cruz-Orize, L.M. (1997). Stereology of Single Objects, J. of Microscopy, 186 pp. 93-107.
Evans, S.M., Janson, A.M, and J.R. Nyengaard (2004). Quantitative Methods in Neuroscience. Oxford University Press, New York.
Gokhale, A.M. (1989). Unbiased estimation of curve length in 3-D using vertical slices. J. Microsc., 159, pp 133-141.
Howard, C.V. and M.G. Reed (2010). Unbiased Stereology Second Edition. QTP Publications, Coleraine, U.K.
Kubínová, L and J. Janácek (1998). Estimating surface area by the isotropic fakir method from thick slices cut in an arbitrary direction. J Microsc. 191(2):201-211.
Mallon, E.B., and N.R. Franks (2000). Ants Estimate Area Using Buffon’s Needle. Proc. Roy. Soc. London B, 267, 765 – 770.
Miles, R.E., and P.J. Davy (1976). Precise and General Conditions for the Validity of a Comprehensive Set of Stereological Fundamental Formulae. J. of Microscopy, 107, 211 – 226.
Saltykov, S.A. (1946). The Method of Intersections in Metallography (in Russian). Zavodskaja laboratorija, 12, 816-825.
Smith, C.S., and L. Guttman (1953). Measurement of Internal Boundaries in Three-Dimensional Structures By Random Sectioning. Transactions AIME J. of Metals, 197, 81 – 87.
Tang, Y. and J.R. Nyengaard (2004). Length Estimation of Nerve Fibers in Human White Matter Using Isotropic, Uniformly Random Sections. Evans, S.M., Janson, A.M, and J.R. Nyengaard, Quantitative Methods in Neuroscience, Chapter 12, Section 1.1, Oxford University Press, Oxford.
Weibel, E.R. (1979). Stereological Methods. Vol. 1. Practical methods for biological morphometry. Academic Press, London.
____________________________________________________________________
Sponsored by MBF Bioscience
developers of Stereo Investigator, the world’s most cited stereology system
