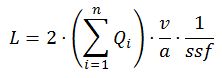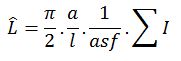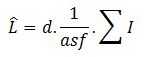Estimating Length of Strings
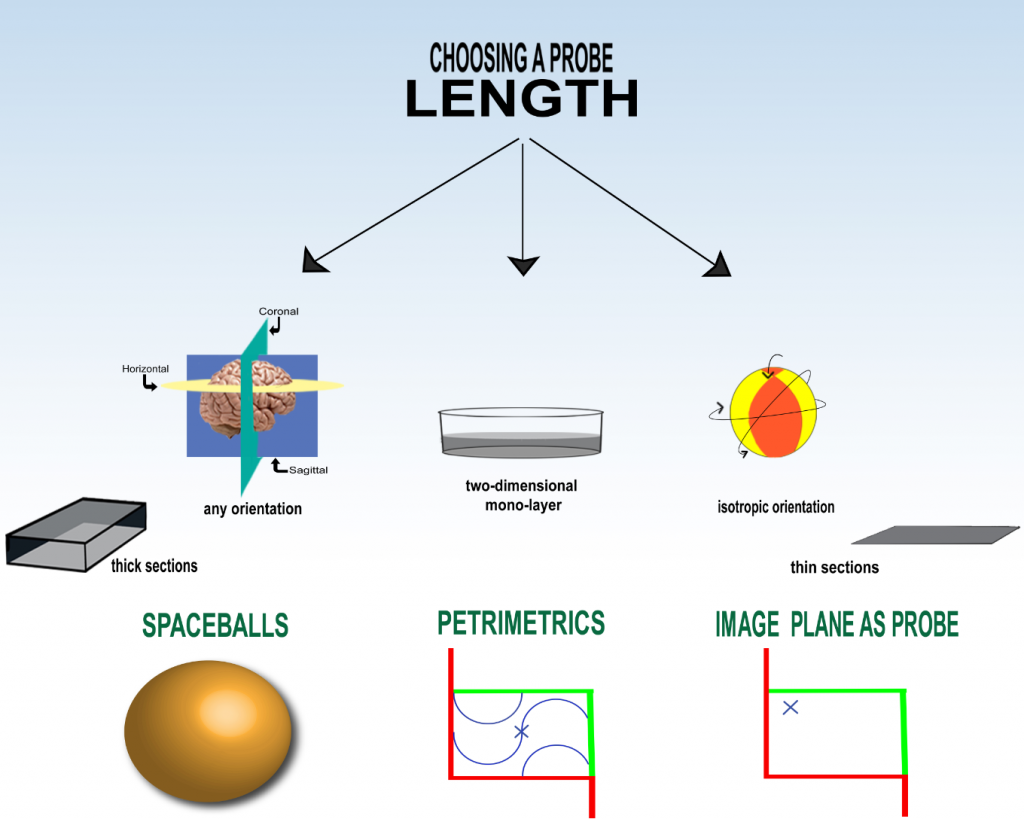
One of the major characteristics that Neuroscientists and those who study other organs are interested in is the length of biological string-like objects, such as nerve fibers or blood vessels (for other types of ‘length’ please see ‘thickness‘ or ‘boundary‘). To obtain an unbiased stereological estimate of length, it’s important to think about the orientation of the strings and of the stereological probe. To probe for length, you must use a 2D geometrical shape that has an area, for example, a plane. The more intersections of the plane with the strings you observe; the longer the length of the strings. Here is the relevant formula:
L v = 2 Q A
where L v is the length of the strings per unit volume, and Q A is the number of intersections of the plane with the strings per unit area (Baddeley and Jensen, 2005, formula 2.11; Howard and Reed, 2010, formula 7.2; also see ‘Buffon’s Needle‘)
But this formula will only yield an unbiased estimate if the strings, or the plane you are probing with, or some combination of the two are randomly oriented in three dimensions (isotropic). To see why this is relevant, look at the following two figures (also see Howard and Reed, 2010, fig. 7.2). Probing for length with a plane when the strings are mostly perpendicular to the probe:
you get a lot of intersections compared to a situation where the strings are parallel to the probe:
some strings pass in front of the plane and some behind, but it’s not likely any will intersect the plane-probe. As we consider probes that can be used to estimate length, we will think about isotropic orientation.
In addition to isotropy, there are two other major factors that influence the choice of probe; whether you have thick sections or thin sections and whether or not you can keep track of the volume fraction (see fractionator principle) during the sectioning.
As always use systematic random sampling.
Spaceballs
If you want to make an estimate of length in your region of interest, the best favor you can do for yourself is have thick sections and keep track of the volume fraction. This makes it possible for you to use the Spaceballs probe (Mouton, et al., 2002) (see Spaceballs, above) in its ‘fractionator’ form. Here the probe itself is isotropic; no matter the orientation of the strings, the surface of the sphere will always encounter them with the same number of intersections. Therefore you can use Spaceballs on preferentially oriented tissue; you don’t have to worry about randomly orienting your tissue.
If you can’t keep track of the volume fraction then the NvVref method must be used (West, 2012, section 5.4.1, Estimating L with the Lv X Vref Method). If you can keep track of the volume fraction, the extrapolation for the estimate is made with this formula:
This formula is in a slightly different form than how it appeared in the original paper; the volume, ‘v’ was defined as the volume of a box that would fit around the isotropic sphere, therefore two more terms, called F2 and F3, were used (Mouton, et al., 2002, equation 2).
For tissue sections that are less than around twenty microns in thickness, a hemisphere instead of a sphere may be used. Only intersections through the convex surface of the hemisphere are counted. The difference in the formula is that the surface area, ‘a’, is that of a hemisphere. Any intersection, Qi, is counted as one-half if the string is penetrating the convex surface of the hemisphere at the level of the cut surface; otherwise we would be over-counting since a hemisphere ‘shares’ its surface with another possible hemisphere. “The isotropy requirement is rigorously complied even if a hemisphere is used instead of a complete sphere to count the intersections” (Mouton, et al., 2002, pg. 60, second column, sixth complete sentence).
Image Plane as the Probe
If you can’t avoid using thin sections, there is no probe for length for tissue that is not random in three planes. Therefore you have to use isotropic tissue. An isotropic section has all three dimensions randomized; the orientation of the tissue sectioning is random so you don’t have to worry about the probe being random. In this case you can use the image through the microscope or the photomicrograph as the plane that is the probe (see ‘image plane as probe’ above). Use random and systematic sampling, as you always should, and a counting frame, and the estimate of length per volume will be twice the intersection number that you count divided by the area. You can use a Fractionator sampling scheme to supply the counting frame and keep track of the intersections of the strings with the image-plane (for examples see Evans et al., 2004, section 3.3, p. 255 and Howard and Reed, 2010, p. 126).
Petrimetrics
If you have a two-dimensional situation, for instance a petri dish, you can use a line probe to probe for the length of strings. In this case please use the Petrimetrics probe (Howard and Reed , 2010, Chapter 12). It employs Merz test-lines that are semi-circles, so you can use preferentially oriented two-dimensional tissue. The fractionator method is used to arrive at the estimate (equation 12.2 in Howard and Reed):
and:
so
Other Length Probes

Spaceballs is at the top of the ‘length tree’ since it uses the fractionator method, can be used on tissue of any orientation, and has rules that are easy to follow (please see text for details).
You could alternatively, use the Isotropic Virtual Planes probe (Larsen, et al., 1998) on thick, preferentially-oriented tissue. This, like Spaceballs, is a case where the probe is isotropic so you don’t have to worry about the orientation of the tissue. Spaceballs has the advantage, however, of being much easier to use.
The L-cycloid optical fractionator probe (Stocks, et al., 1996) and the IUR planes optical fractionator probe (Howard and Reed, 2010, Chapter 7) are also used on thick tissue, but are not suitable for preferentially oriented tissue; the former calls for tissue that is random in two planes, vertical sections, and the latter for tissue that is random in three planes, isotropic sections.
Another method you can use for length estimation is the Cycloids for Lv probe (Gokhale, 1989). Thick sections that are random in two planes are required, but you can use this probe without keeping track of the volume fraction. However it is always better to keep track of the volume fraction and extrapolate to get the estimate, so if at all possible, please use the Spaceballs probe.
Baddeley, A. and E.B.V. Jensen, 2005 Stereology for Statisticians, CRC Press, Boca Raton, FL, USA
Evans, S.M., A.M. Janson, J.R. Nyengaard, 2004 Quantitative Methods in Neuroscience, Oxford University Press, Oxford, U.K.
Gokhale, A.M. 1989 Unbiased estimation of curve length in 3-D using vertical slices. J. Microsc., 159, pp 133-141.
Howard, C.V. and M.G. Reed, 2010, Unbiased Stereology, Second Edition QTP Publications, Liverpool, U.K.
West, M.J. (2012) Basic Stereology for Biologists and Neuroscientists, Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY
____________________________________________________________________

Sponsored by MBF Bioscience
developers of Stereo Investigator, the world’s most cited stereology system