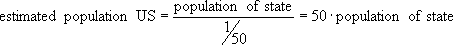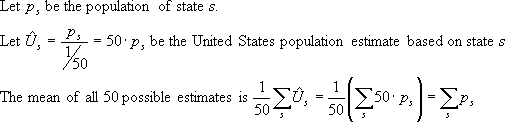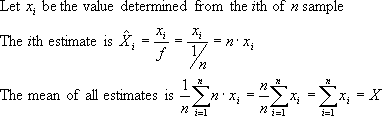The fractionator principle is one of the important concepts used in stereology. The importance of this principle cannot be overlooked. It appears in many different places. Although it looks different depending on how it is used, the principle is the same.
The fractionator principle states that if you take as a random sample a known fraction of a population, then the unbiased estimate for the population is the value from the sample divided by the fraction. The mathematical formula for this is:
Figure 1. The basic Fractionator formula.
The symbol X represents the quantity of interest. It might be numbers of things, volume, or whatever is under study. The X with the caret is the estimate of X. The lowercase x is the value, either measured or estimated, from the sample. f is the fraction sampled. It is important to point out that this estimate of X is only unbiased if the value x is also unbiased.
The fraction f is easy to obtain. The researcher selects it. The appropriate value for f depends on the balance between the amount of work that needs to be done and the accuracy of the estimate obtained. The fraction f ranges between 0 and 1. Of course, f must be larger than 0 otherwise nothing is sampled. When the fraction is 1, the entire population is the sample (exhaustive sampling).
The researcher arbitrarily chooses the fraction. It does not have to be random, and it should not be. For example, if the population is cells to count and there are billions of cells, then it makes sense to have a small fraction say about 1/10,000,000. Such a small fraction means that the sample is a small enough number of cells to be reasonable. Being able to reduce the work to a reasonable level is an important part of the criteria for choice of a fraction. Another important issue is the variance of the estimate, which is how satisfactory the estimate is. That issue is explored later (see Study Design).
Consider the following example of the fractionator. Suppose the population of a country is of interest. In this example, we estimate the population of the United States. To estimate the population of the United States, we apply the fractionator principle. The fraction is chosen to be 1/50. That fraction is chosen since there are 50 states in the United States. To apply the fractionator principle one state is chosen randomly and the population of that state is determined. Suppose that the randomly chosen state is Missouri. Missouri had a population of 5,595,211 in a recent census. Using the fractionator principle, the estimated population of the entire United States is 279,760,550. The actual population of the United States from that same census turned out to be 280,849,847.
The mathematical formula for this is:
Figure 2. Formula to estimate the population of the United States of America.
That seems like a good estimate based on the tallies from one state. California, the most populous state had as much of a chance as being randomly selected as Wyoming, the least populous state. Had we selected California then the estimate would have been 1,693,582,400. Had Wyoming been the randomly selected state then the population estimate for the United States would have been 24,689,100. That is a large spread for the estimates.
Let us examine a few important issues about this estimate. First, we need to investigate the concept of bias. Bias simply means that the average of all samples is not going to be the right answer. Another way of looking at this is to say that the more work done, the more certain we become that the estimate is wrong. The fractionator claims that the answer is unbiased. Therefore, the more work done the more the answer converges to the true value.
As stated above, the fractionator principle states that if you randomly sample a known fraction of a population, then the unbiased estimate for the population is the value from the sample divided by the fraction. The mathematical formula for this is:
Figure 3. Unbiased for mula for estimating the population of the United States of America.
The math shown here says that the average of all 50 possible estimates works out to be the population of the United States. This shows that the fractionator principle in this case is unbiased.
Two things should be clear so far:
1. The estimate derived from the fractionator principle is unbiased
2. The estimate may not be close to the true answer
The basis for the selection of the fraction for the population estimate of the United States was a simple means of breaking up the population of the entire country into a more manageable size.
Another way of reducing the work is to pair the states. This changes the fraction f to 1/25. One way of doing this might be to pair the states up is to list them in alphabetical order and then pair up consecutive states. Another way is to pair the states up according to size. Suppose that we list the states in the order that begins with the state believed to have the smallest population on up to the state with the largest population. Notice that before the census is taken it is not to actually know the proper order of the states, but a reasonable ordering can be laid out. The first and last state can be paired. Next, the second and next to last are paired. This continues until all states are paired. Another ordering from this list might be to take the first and 26th states, the second and 27th, and so forth until the 25th and 50th are paired.
| method | smallest estimate | largest estimate | standard deviation | average estimate |
| Selecting a state at random | 24,689,100 | 1,693,582,400 | 309,278,978.9 | 280,849,847 |
| Pairing states from alphabetical list | 125,274,500 | 1,908,645,450 | 439,566,379.7 | 280,849,847 |
| Pairing opposite ends of a sorted list | 192,188,500 | 859,135,750 | 153,961,360.3 | 280,849,847 |
| Pairing every 25th in the sorted list | 113,388,775 | 947,091,500 | 195,691,178.3 | 280,849,847 |
A quick inspection of the results shows that all of the methods are unbiased, which means that the average result is the correct answer. It is also clear that the answers range wildly. The largest and smallest estimates form a wide range. The standard deviation column also hints at the spread of the estimates. The smallest standard deviation comes from the method that attempts to use samples related to the value being estimated.
This example shows several things.
1. Unbiased does not mean accurate, nor does a wide spread of estimates mean bias.
2. You can apply the fractionator principle to many different fractions and many ways of forming any one fraction.
3. The format of the experiment can be used to control the random error due to sampling.
Figure 4. Unbiased Fractionator formula.
This simple derivation shows that the average of the estimates made with the fractionator is indeed the true result. The reason that we refer to this form of the fractionator principle as being 1 dimensional is that the samples are taken from a list. The values can also be taken along an axis.
____________________________________________________________________

Sponsored by MBF Bioscience
developers of Stereo Investigator, the world’s most cited stereology system