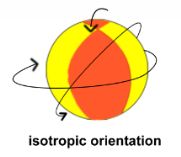
The combination of marking points and intercepts can be used to estimate respectively, the area (Howard and Reed, equation 3.2) and the boundary (B) (Howard and Reed, equation 2.5) of the cross section of a three dimensional object. The tissue must be isotropic (Howard and Reed, p. 34, last paragraph, second sentence).
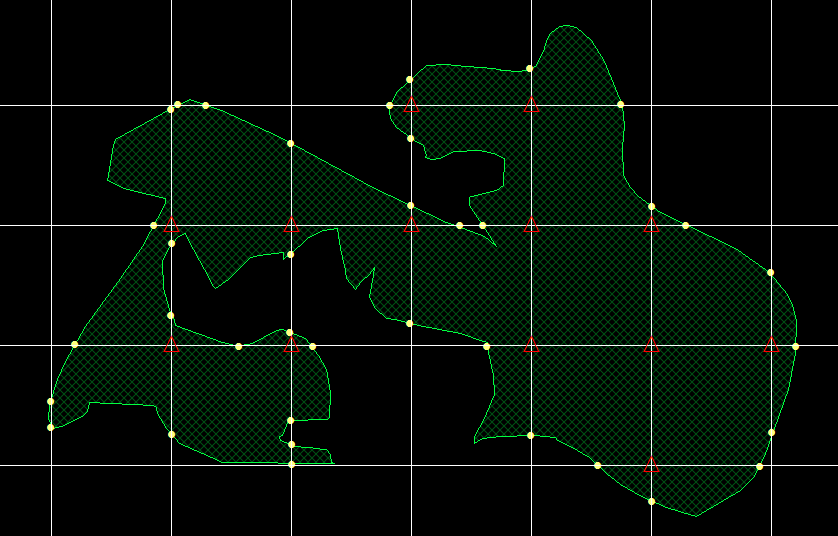
A grid of known dimensions is used to probe for both area and boundary-length. For the estimate of area, the vertices of the grid are the points, and they are marked when they land on the cross section of the 3-D object (red open triangles). For the estimate of boundary-length, the intersection of the grid with the surface of the object is marked (yellow circles). Always use systematic random sampling.
Area
a = a(p) ∑ P (Howard and Reed, equation 2)
a = estimate of the area of the cross section of 3-D object
a(p) = area associated with each point (area of one grid box)
∑ P = number of points (yellow circles in example above) marked
Boundary
B = π/2 (d) ∑ I (Howard and Reed, equation 2.5)
B = length of boundary of cross section of 3-D object
d = length of one side of one grid box (d2 = a(p))
∑ I = number of intersections (open red triangles in example above)
Usually, however, it is the surface or the surface per volume of the three dimensional object that is of interest, not the boundary of the cross section.
Howard, C.V. and M.G. Reed (2010) Unbiased Stereology Second Edition. QTP Publications, Coleraine, U.K.