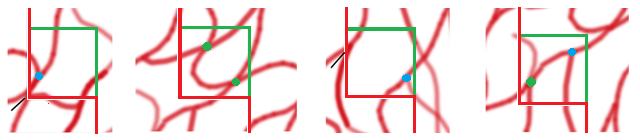Review of Publication: Wälchli, T., Mateos, J.M., Weinman, O., Babic, D., Regli, L., Hoerstrup, S.P., Gerhardt, H., Schwab, M.E., and J. Vogel (2015) Quantitative Assessment of Angiogenesis, Perfused Blood Vessels and Endothelial Tip Cells in the Postnatal Mouse Brain. Nature Protocols, 10, 53 – 74.
The next manuscript we will look at is also a very well written guide to using unbiased stereology to estimate cardinal parameters of the vasculature. Unlike the paper on thin sections reviewed here (Mühlfeld, 2014) however; this review (Wälchli, et al., 2015) considers how to quantify vasculature in thick, forty micron sections instead of thin, two to three micron sections. Isotropic probes can be used in thick sections when estimating length and surface, eliminating the need to make the tissue isotropic. In other words, instead of having to use isotropic or vertical sections when making length and surface estimates as is the case for thin sections, the authors’ preferred orientation, in this case coronal (Wälchli, et al., “PROCEDURE, step 33, first critical step”), can be used!
The post-natal mouse brain is an interesting model system to study angiogenesis since it is ongoing after birth (Wälchli, et al., “Toward mature, perfused blood vessels: the postnatal mouse brain as a model”). Perfused blood vessels and non-perfused blood vessels were differentiated to look at ‘perfusion status’. Evans Blue (EB) that binds to serum albumin was injected intracardially on post natal day eight to label perfused blood vessels but not non-perfused vessels. Brains were removed and sectioned coronally into three slabs and fixed and then treated for isolectin B4 (IB4) that binds to endothelial cells, thus revealing both perfused and non-perfused vessels. The authors ”recommend the use of relatively thick (e.g., 40-μm) brain sections to obtain reliable 3D information about the blood vessel tree and to quantify vessel parameters such as vessel volume fraction, vessel length or vessel branch points (Fig. 5).” (Wälchli, et al., “Experimental design, last paragraph, also see, PROCEDURE, step 17”).
Systematic random sampling for choosing the inter-section and the intra-section interval is also recommended. Confocal laser-scanning microscopy image stacks were taken. Analysis of perfused and non-perfused vessel structure using unbiased stereology to determine, volume fraction, length and number of branch points and endothelial tip cells was done with a 20x objective (Wälchli, et al., “Imaging and quantification”). This is fine for all of these analyses except for estimating number, where a higher numerical aperture lens (0.13 or 0.14) should be used.
It is stressed that design-based stereological methods
provide direct information about morphological 3D parameters of interest — e.g., the length of vessels, the number of vessel branch points or the vessel volume fraction. This is in stark contrast to the biologically difficult-to-interpret but commonly used variety of measures such as ‘percent of the area of a section occupied by vessels’, ‘number of pixels occupied in an image’ or ‘measures of length or diameter’ in 2D projections. (Wälchli, et al., “Imaging and quantification, second paragraph”; also see, “Advantages of the protocol compared with alternatives, fourth and fifth bullet-point”).
The easiest way to measure is to count the interactions between vascular features and geometric probes — i.e., how many times does a test point fall onto the volume of a vessel, how many times does the length of a vessel intersect with a test area or how many vessel branch points are contained in a volume probe? (Wälchli, et al., “Imaging and quantification, fourth paragraph”).
The NvVref method used requires that an estimate of numerical density (Nv) such as surface per volume, is multiplied by the reference volume (Vref) to avoid the volume-reference trap. The fractionator method could have been used if the volume fraction could have been tracked. Our software package, StereoInvestigator, is used, giving the “advantage that all calculations are taken care of.” (Wälchli, et al., “Imaging and quantification, fourth paragraph”).
“Aside from their rigorous mathematical basis and efficiency, design-based stereological methods provide access to parameters that would otherwise be difficult, if not impossible, to accurately measure in tissue sections.” (Wälchli, et al., “Imaging and quantification, fifth paragraph”). The example of capillary segment length is considered. For direct measurements, the entire segment would have to be contained within a section. “Shorter capillary segments would be more likely to be included in the section than longer ones, always generating an underestimate independent of orientation and shape.” (Wälchli, et al., “Imaging and quantification, fifth paragraph”). Counting intersections of the vessels with the image plane is possible, but isotropy must be ensured or the risk of “potentially biasing estimates to capillary segments with a preferred orientation (in the section plane)” is incurred.
Any experimental intervention that alters the orientation or shape of capillary segments, i.e., 3D vascular architecture, has the potential to change the estimates of segment length in an unpredictable direction and with unpredictable strength, and, most importantly, without the need for an actual change of length to be present. Aside from obviating the need to generate a sufficiently large sample of capillary segments included in the section plane in the first place, the combination of stereological length estimates with branch-point counts to derive segment length is free from these potential biases. (Wälchli, et al., “Imaging and quantification, fifth paragraph”).
The procedure for using unbiased stereology for quantification of the vasculature (Wälchli, et al., “PROCEDURE, step 33, and Figure 5”), is very well laid-out. Events are counted,
i.e., points for vascular volumes, areas for vascular lengths and volumes for vascular branch points. Use design-based stereological methods, because the resulting estimates are unbiased in the sense that the number of interactions is independent of the size, shape or orientation of vascular features other than those of the feature of interest. (Wälchli, et al., 2015, PROCEDURE, step 33, first paragraph)
It is a critical step to define the region of interest on the section that was selected by systematic random sampling. Instead of contouring the whole cortex in the given section, ‘a complete cortical transect from the pial surface to the deep border of the layer 6 of a 40-um-thick coronal brain section’ is outlined (Wälchli, et al., “PROCEDURE, step 33, first critical step”); in Figures 5a-c, it is apparent the whole cortex is not traced, and this adds a random element to the otherwise systematic and random sampling. Since the volume fraction is not kept track of at this point, the fractionator method is not possible so the NvVref method must be used. Systematic random sampling is used in the randomly selected region of cortex to determine where confocal stacks are taken.
Vessel Volume Fraction (Wälchli, et al., “PROCEDURE, step 33A”)
The Area Fraction Fractionator probe, (all probes were implemented in our software, StereoInvestigator), is used to estimate the percent of perfused and non-perfused blood vessels by volume. An example of marking points on the three types of tissue; perfused blood vessels, non-perfused blood vessels, and non-blood vessel tissue, is shown in figures 5d and 5g. The point-marking is done on one confocal image plane; it is pointed out that will minimize over-projection problems since this plane is so thin, 0.2 microns. The plane is picked randomly from the stack.
Vessel Length (Wälchli, et al., “PROCEDURE, step 33B”)
The Spaceballs probe was used to estimate length density of perfused and non-perfused blood vessels. If the fractionator method had been used, there would be no need to know the reference volume that has to be multiplied by the numerical density to obtain a length estimate. In figures 5e and h, an example of marking the intersection of the ‘backbone’ of a vessel with the virtual hemisphere is shown. The hemispheres were twenty microns in radius to fit inside the tissue sections. The hemisphere is itself isotropic, so the tissue does not have to be manipulated (see vertical and isotropic sectioning); the huge advantage of using thick sections when estimating length is that an isotropic probe is possible allowing the use of preferentially oriented, in this case coronal, sections.
Vascular Branch Point and Vascular Endothelial Tip Cell Number (Wälchli, et al., “PROCEDURE, step 33C and D”)
The Optical Disector (NvVref method) was used to count nodes in perfused and non-perfused vessels and also to count tip cells. An example of marking these objects in a twenty micron tall disector is shown in figures 5f and i. Thick sections must be used for this probe so the disector can fit inside the section. For nodes, each is categorized with a valence, indicating how many segments come out of that node; only nodes with three or four branches were encountered.
Calculating Number of Segments and Other Vascular Parameters (Wälchli, et al., “PROCEDURE, step 33E”)
The parameters that were estimated (see above) can variously be used to calculate other information:
Number of Microvessels (Løkkegaard, et al., 2001, “Number”)
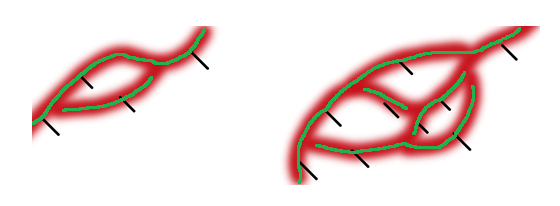
If we know the estimate of the number of nodes, Pn, of a given valence, n, we can calculate the number of microvessels, W, and number of segments, s (Løkkegaard, 2004, “Chapter 7, Fig. 7.3”).
In the figure above, counting frames are shown, and a unique point has been determined to count, i.e., the cusp of the smallest angle. The diagonal black dashes show where a node has been ruled out since its unique point goes through the rejection plane of the disector shown here as the red-line of a counting frame. The blue circles indicate nodes with valences of three, because they have three branches coming from them, and the green circles indicate nodes with valences of four.
The number of capillaries (number of microvessels) is:
W = ∑ {[(n-2)/2] * Pn} + 1
W is the number of microvessels
n = valence of the nodes
Pn = number of nodes of that valence
If using the NvVref method instead of the fractionator method, divide by the sum of the volumes of all the disectors and then you must multiply by the reference volume.
The example on the left has two nodes, each with valences of three. The vessels are shown in red.
W = (3-2)/2 * 2 + 1 = 2
In other words you can trace two paths without going over the same vessel. An example of two paths making up two capillaries or microvessels is shown in green.
The example on the right has four nodes each with a valence of three, and one node (the node farthest to the right) with a valence of four.
W = [(3-2)/2 * 4] + [(4-2)/2 * 1] + 1 = 2 + 1 + 1 = 4
In other words we can trace four paths (one example is shown with the green traces) through the network without going over the same vessel twice.
Number of Segments (Løkkegaard, et al., 2004, “Fig. 7.3”)
Once the number of microvessels is know, we can calculate the number of segments:
S = W + ∑ nv
S is the number of segments defined as from one node to the next
W = number of microvessels (see green traces)
nv = number of nodes of all valences
For the example on the left there are two nodes and two microvessels (W = 2, green lines):
S = 2 + 2 = 4
Each of the four segments is indicated with a diagonal-dash.
For the example on the right, there are four nodes with valence three, and one with valence four, so the sum of all nodes regardless of valence is five. The number of microvessels, W, is four.
S = 4 + (4 + 1) = 9
The nine capillary segments are indicated by nine diagonal dashed lines.
Average Capillary Length (Løkkegaard, et al., 2001, p. 732)
The average capillary length can be calculated by dividing the estimate of the length of all capillaries by the number of microvessels. In the Løkkegaard paper that is referenced (Løkkegaard et al., 2001), the total length estimate is made with thin sections that have been made isotropic with the use of the isector. This is at least partially because Spaceballs was not invented yet!
l-mean (cap.) = L(cap)/W(cap)
l-mean (cap.) is the mean length of microvessels
L(cap) = total length estimate obtained with Spaceballs (see above)
W(cap) = number of capillaries (microvessels) (see above)
Average Diffusion Area and Radius (Løkkegaard, et al., 2001, p. 732)
The estimate of length density of vessels obtained with Spaceballs can be used to calculate the average diffusion area of the vessels:
A(diffusion) = 1/Lv
A(diffusion) is area of cortex associated with the length of the vessels
Lv = length of vessels per volume of cortex estimated with Spaceballs
If we model the volume along the vessel as a cylinder, we can ‘work backwards’ and calculate the radius associated with that cylindrical volume:
Volume of a cylinder = π * r2 * length
radius(diffusion) = square root [Volume of a cylinder / π * length] = square root [1/ π * Lv]
radius(diffusion) is the length along the vessel in all radial directions that constitutes the volume of cortex associated with that vessel
Lv = length density estimate obtained with Spaceballs
The surface of the inner wall of the vessels can also be calculated by working backwards from the formula for the surface of a cylinder (Løkkegaard, et al., 2001, p. 732). But to estimate surface directly, the isotropic fakir probe could have been used. Analogous to Spaceballs, it is a probe that is itself isotropic requiring thick sections but allowing for the use of preferentially oriented sections.
References
Løkkegaard, A., Nyengaard, J.R., and M.J. West (2001) Stereological Estimates of Number and Length of Capillaries in Subdivisions of the Human Hippocampal Region, Hippocampus, 11, 726-740
Lokkegaard , A. (2004) The Number of Microvessels Estimated by an Unbiased Stereological Method Applied in a Brain Region. Chapter 7 in Quantitative Methods in Neuroscience: A Neuroanatomical Approach . Evans et al., 2004. Oxford University Press.
Wälchli, T., Mateos, J.M., Weinman, O., Babic, D., Regli, L., Hoerstrup, S.P., Gerhardt, H., Schwab, M.E., and J. Vogel (2015) Quantitative Assessment of Angiogenesis, Perfused Blood Vessels and Endothelial Tip Cells in the Postnatal Mouse Brain. Nature Protocols, 10, 53 – 74.